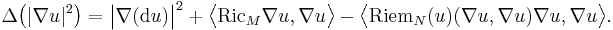Bochner identity
In mathematics — specifically, differential geometry — the Bochner identity is an identity concerning harmonic maps between Riemannian manifolds. The identity is named after the American mathematician Salomon Bochner.
Contents |
Statement of the result
Let M and N be Riemannian manifolds and let u : M → N be a harmonic map. Let d denote the exterior derivative, ∇ the gradient, Δ the Laplace–Beltrami operator, RiemN the Riemann curvature tensor on N and RicM the Ricci curvature tensor on M. Then
References
- Eells, J; Lemaire, L. (1978). "A report on harmonic maps". Bull. London Math. Soc. 10 (1): 1–68. doi:10.1112/blms/10.1.1. MR495450.
External links
- Weisstein, Eric W., "Bochner identity" from MathWorld.